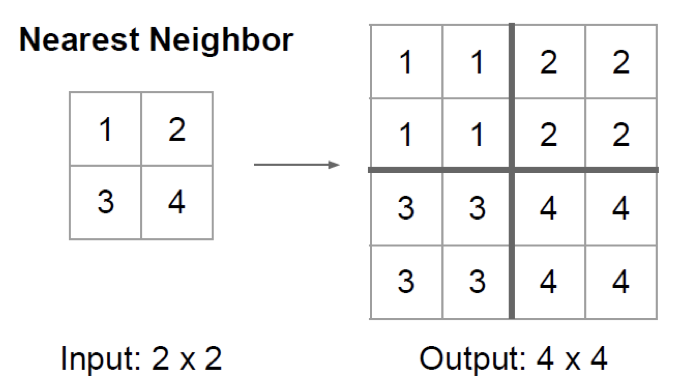
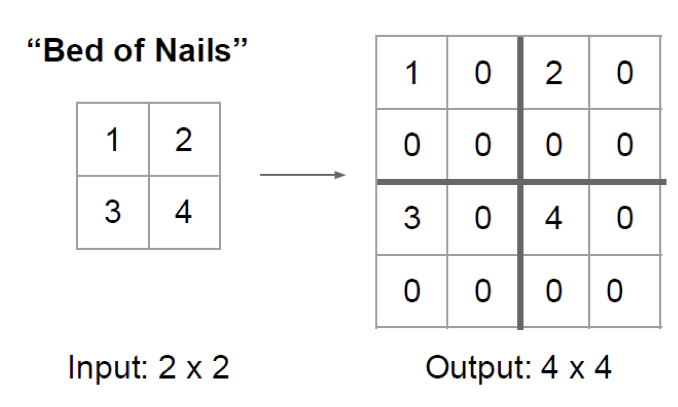
上采样
- 将图像采样到更高的分辨率(由小分辨率到大分辨率)
- 将高维特征进行放大
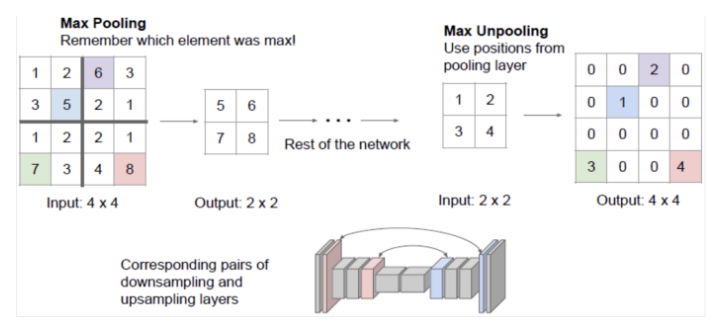
Unpooling
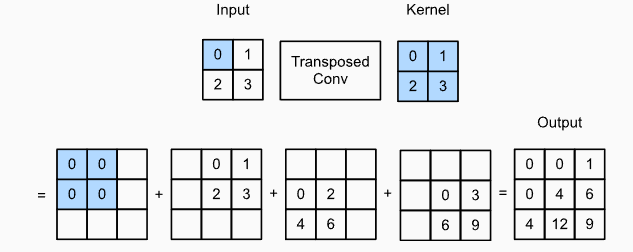
Transposed Convolution (转置卷积)
- 对特征进行padding,然后进行卷积
- Output_size = (input_size -1) * stride + filter - 2 * same padding + output padding
def trans_conv(X, K):
h, w = K.shape
Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Y[i: i + h, j: j + w] += X[i, j] * K
return Y
高斯滤波
-
对整幅图像进行加权平均的过程,每一个像素点都由本身和领域内的其他像素值加权平均后得到
-
可以用于消除图像中的高斯噪声
-
高斯滤波只考虑了相邻像素空间位置层面的影响,没有考虑值域的影响
$$ G[I]{p} = \sum{q\in S}G_\sigma(\Vert p-q \Vert)I_q $$
$$ q : \text{邻域空间} \quad G_\sigma(x) : 2d \text{高斯核} $$
高斯噪声
- 概率密度服从正态分布的一类噪声
- 高斯白噪声:功率谱密度为均匀分布
高斯函数
- 一维高斯分布
$$ G(x)= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}} $$
- 二维高斯分布 $$ G(x, y)= \frac{1}{\sqrt{2\pi}\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} $$
高斯核
- 根据坐标计算高斯模板
- 保证高斯模板加起来为1
- 输入图像乘以相关核
- 相加得到中心点的高斯滤波的值
- 方差$\sigma$决定了滤波的范围
双边滤波
-
不仅考虑了空间位置的影响,还考虑了值域的影响,能够很好的保留边缘信息
-
双边滤波器移除了部分噪声和纹理特征
$$ BF[I]{p} = \frac{1}{W_p}\sum{q\in S}G_{\sigma_s}(\Vert p-q \Vert)G_{\sigma_r}(\vert p-q \vert)I_q $$
$$ W_{p} = \sum_{q\in S}G_{\sigma_s}(\Vert p-q \Vert)G_{\sigma_r}(\vert p-q \vert)I_q $$
Retinex Theory
-
理论基础:物体的颜色不受光照非均匀性的影响,具有一致性,以颜色恒常性为基础
-
通过对原始图像进行高斯滤波来获取照度图像,最后将照度图像从原始图像分离出来,从而获得反射图像
-
原始图像$I(x,y)$可被表示为为入射分量$L(x,y)$和反射分量$R(x,y)$的乘积
- $L(x,y)$: 环境光的照射分量
- $R(x,y)$: 携带图像细节信息的目标物体的反射分量
-
从原始图像$S(x,y)$估计出光照分量$L(x,y)$, 从而分解出反射分量$R(x,y)$, 消除光照不均的影响
-
照度估计:将图像转换到对数域对整幅图像求均值
$$ R(x,y) \approx log(I(x,y))-log(F(x,y)*I(x,y)) $$
$$ *: Convolution \quad F(x,y):Surrouding \quad function $$
-
Single-scale Retinex(SSR)
$$ SSR_i(x,y)=log(I_i(x,y))-log(G_\sigma*I_i(x,y)) $$
$$ i \in R,G,B \quad G_\sigma(x,y) = Ke^{-\frac{x^2+y^2}{2\sigma^2}}\quad \int\int G_\sigma(x,y)dxdy =1 $$
- Multi-scale Retinex(MSR) $$ MSR_i(x,y,\sigma_k) = \sum_{k=1}^nw_kSSR_i(x,y,\sigma_k) $$
亮度直方图
- 关于灰度级的分布函数,灰度值范围$[0, 255]$
- 将图像种所有的像素点,按照灰度值的大小,统计其出现的频率
AdaIN(Adaptive Instance Normalization)
-
自适应实例标准化
-
将Content image(x)特征的均值和方差对齐到Style image(y)的均值和方差
-
特征的均值和方差代表着图片的风格 $$ AdaIn(x,y) = \sigma(y)(\frac{x-\mu(x)}{\sigma(x)})+\mu(y) $$
Log & Exp
-
Log 操作:压缩图像对比度,使图像变得模糊 $$ s = c * log(1+r) \quad c = 255/(log(1+max(r))) $$
$$ r: \text{输入像素} \quad c:\text{缩放常数} \quad s:\text{输出像素} $$
-
Exp操作:拉伸对比度
import cv2
import numpy as np
img = cv2.imread()
img_log = (np.log(img+1)/(np.log(1+np.max(img))))*255
img_log = np.array(img_log,dtype=np.uint8)
cv2.imshow('log_image',img_log )
cv2.imshow('original_img',img)
cv2.waitKey(0)
图像的空域和频域
导数
- 一阶导数 $$ \frac{\partial I}{\partial x} = I(x+1, y) - I(x, y) $$
$$ \frac{\partial I}{\partial y} = I(x+1, y) - I(x, y) $$
-
二阶导数 $$ \frac{\partial^2 I}{\partial x^2} = I(x+1, y) - I(x-1, y)-2f(x,y) $$
$$ \frac{\partial^2 I}{\partial y^2} = I(x, y+1) - I(x, y-1)-2f(x,y) $$
$$ \nabla^2I = I(x+1, y) - I(x-1, y) +I(x, y+1) - I(x, y-1)-4f(x,y) $$
- 可根据二阶导系数得到$Laplacian \quad Filter$
灰度化
- 使得彩色图像的$R,G,B$分量相等的过程
图像的频率
- 表征图像中灰度变化剧烈程度的指标
- 灰度变化缓慢(低频)灰度变化剧烈(高频)
- 高频决定细节(边缘),低频决定总体形状
- 图像的空域乘积等于频域卷积
- 图像的空域卷积等于频域乘积(频域乘积:频率函数$\times$滤波函数)
傅里叶变换
- 傅里叶变换:只能获取一段信号总体上包含哪些频率成分,但是对各个成分出现的时刻不知道
- 无法处理非平稳信号
- 将图像信号分解为不同频率的正弦波,得到不同频率下正弦波的系数
小波变换
-
短暂的震荡波(母带信号:Haar, Morlet, Daubechies)
-
将图像信号分解为由母带信号缩放和位移之后的一组小波,得到不同尺度小波下的系数
$$ X(a, b) = \frac{1}{\sqrt{a}}\int_{-\infty}^{\infty}\psi(\frac{t-b}{a})x(t)dt $$
$$ a:\text{Sacling factor} \quad b: \text{Time shift} $$
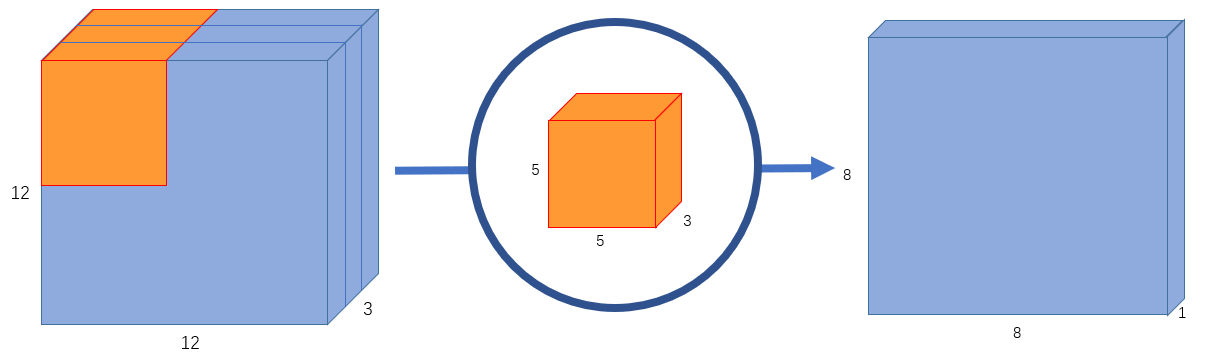
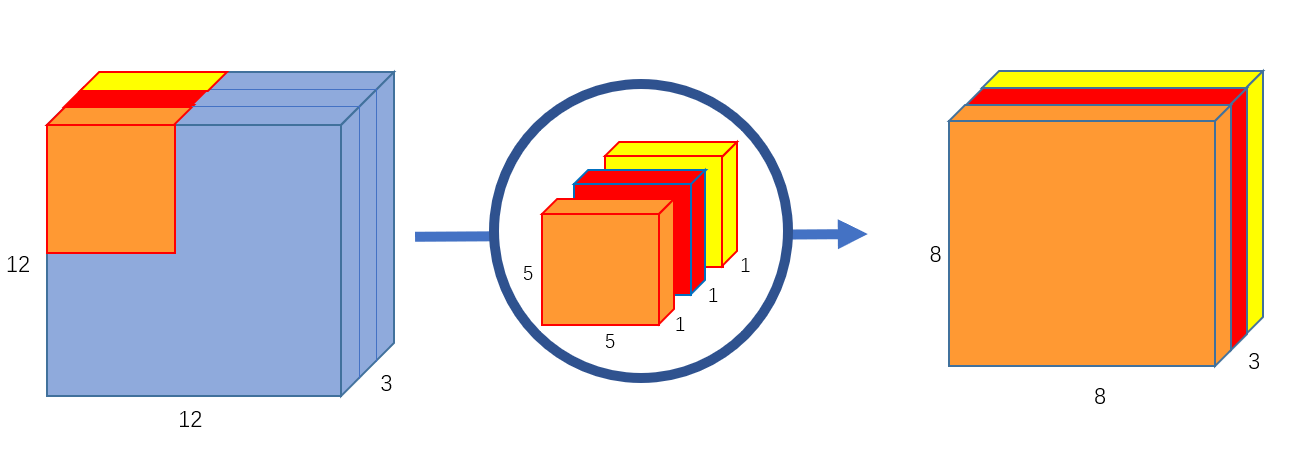
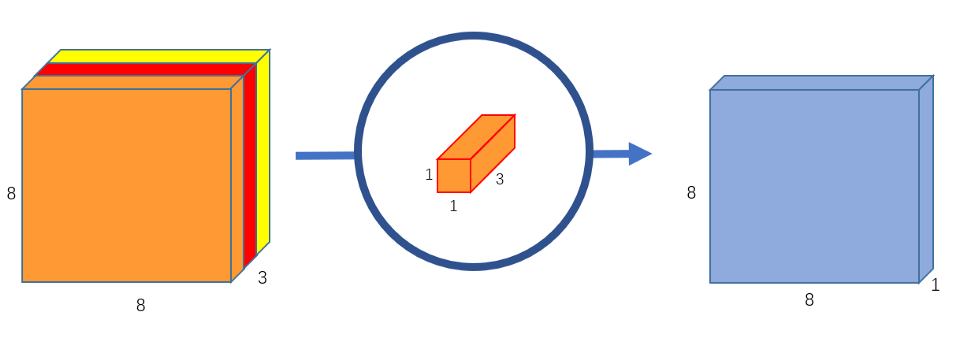
Convolution
- Normal Conv
图像基础
- 动态范围:最大可度量灰度与最小可检测灰度之比,建立了一个系统能够表示衣服图像所具有的最低和最高灰度值
- 上限取决于饱和度,下限取决于噪声
- 饱和度:指一个最大值,超过这个该值的所有灰度值都将被裁剪掉
- 对比度:最高灰度和最低灰度级间的灰度差