查找算法

• 平均查找长度(ASL)
  • $ASL = P_i * \sum C_i$
    • $P_i$: 第$i$​个数据元素的概率
    • $C_i$: 找到第$i$​个数据元素已比较过的次数
• 顺序查找
  • $ASL = 1/n * (1+2+\dots +n) = \frac{n+1}{2}$
  • 时间复杂度$O(n)$
• 二分查找

  • 最坏$k$次二分找到

  • 时间复杂度$O(logn)$​

  • $mid = (right+left) // 2$

  • 数据元素必须有序

  • 防止溢出：$mid = left + (right-left) // 2$​

    if num < list[midpoint]:
    	right = midpoint-1
    else:
    	left = midpoint+1
    

排序算法

• 冒泡排序

  • 对无序表进行多次比较交换

  • 算法复杂度为$O(n^2)$​

    for i in range(len(list)-1, 0, -1):
        for j in range(i):
            if list[j] > list[j+1]:
                list[j], list[j+1] = list[j+1], list[j] 
    

    for i in range(len(list)-1): # 冒多少次
        for j in range(len(list)-1-i): # 冒泡的方向
    
    

• 选择排序

  • 每次仅进行一次交换，记录最大项的所在位置，再和本次的最后一项进行交换（只进行一次交换）

    for i in range(len(list)-1, 0, -1)：
    	max_pos = 0
        for j in range(1, i+1):
            if list[j] > list[max_pos]:
                max_pos = j
        temp = list[i]
        temp[i] = temp[max_pos]
        list[max_pos] = temp
    

    

• 插入排序

  • 算法复杂度为$O(n^2)$

  • 维持一个已经排好序的子列表，不断扩充子列表直到全表

    for index in range(1, len(list)):
        cur_val = list[index]
        pos = index
        while pos>0 and list[pos-1]>cur_val:
            list[pos] = list[pos-1]
            pos = pos-1
        list[pos] = cur_val
    

    

• 归并排序

  • 递归算法，将数据表持续分裂为两半，对两半进行归并排序

  • 复杂度为$O(nlogn)$

    def merge_sort(list)
    	if len(list)<=1:
            return list
    	mid = len(list)//2
    	left = merge_sort(list[:mid])
        right = merge_sort(list[mid:])
        merged = []
        while left and right:
            if left[0] < right[0]:
                merged.append(left.pop(0))
            else:
                merged.append(right.pop(0))
        merged.extend(right if right else left)
        return merged
    

• 快速排序

  • 递归算法，依据一个“中值”数据将数据表分为两半：小于“中值”的一半和大于“中值”的一半，每一部分进行快速排序

  • 选定中值

  • 左标右移，右标左移，左标遇到数比中值大就停止，右标遇到比中值小就停止，交换左右标的值，两标相错就结束移动

  • 算法复杂度为$O(nlogn)$

    

    def quicksort(arr_, left_index, right_index):
    	if left_index >= right_index: return
    	i, j = left_index, right_index
    	while i < j:
            # 左端为哨兵元素
            # 最后i和j指向同一个小于哨兵元素的元素
            while i< j and arr_[j] >= arr_[left_index]: j -= 1 
            while i < j and arr_[i] <= arr_[left_index]: i += 1
            arr_[i], arr_[j] = arr_[j], arr_[i] 
    	arr_[i], arr_[left_index] = arr_[left_index], arr_[i]
    	quicksort(arr_, left_index, i-1)
    	quicksort(arr_, i+1, right_index)
    quicksort(arr, left, right)
    

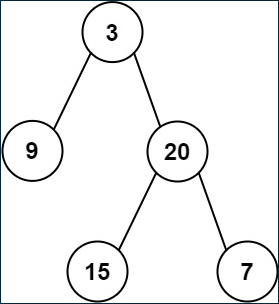
二叉树的遍历

• 前序遍历：根左右
  • 3-9-20-15-7
• 中序遍历：左根右
  • 9-3-15-20-7
• 后序遍历：左右根
  • 9-15-7-20-3
• 前序遍历和中序遍历可以还原二叉树
• 前序遍历和后序遍历不可以还原二叉树
• 完全二叉树
  • 叶节点最多出现在对底层和次底层
  • 最底层的叶节点都集中在最左边
  • 每个节点都有两个子节点，最多可以有一个节点例外
• 二叉查找树
  • 左子树的值比父节点小，右子树的值比父节点大

优先队列

• 最大优先队列，无论入队顺序，当前最大的元素优先出队
• 最小优先队列，无论入队顺序，当前最小的元素优先出队
• 二叉堆能保证优先队列的入队和出队复杂度都保持在$O(log n)$
  • 保持在对数数量级上，需要保持二叉树的“平衡”——左右子树拥有相同数量的节点
• 堆
  • 堆中所有节点的值必须大于或等于其孩子节点的值
  • 当树的高度h大于0时，所有叶子节点都位于第h层或者第h-1层

递归

• 结束条件
• 减小规模
• 调用自身

快速幂

• 判断n的最右一位是否位1：$n$ & 1
• $x^n = x^\frac{n}{2}\times x^\frac{n}{2} = (x^2)^{\frac{n}{2}}$
• 时间复杂度为$O(logn)$

回溯法

• 组合， 切割，子集，排列，棋盘问题

Backtracking(xxx):
	if(终止条件)：
		收集结果
		return
	for(集合元素)：
		处理节点
		递归函数
		回溯操作

摩尔投票法

• 数组中每个元素都可以成为候选，维持一个count，如果元素和候选相同，count加一，否则减一，候选可变

   count, result = 0, 0
          for i in nums:
              if count == 0:
                  result = i
              if result == i:
                  count += 1
              else:
                  count -= 1
          return result
  

遍历子序列或者子串

• 以某个节点为开头的所有子序列: 如 [a], [a, b], [a,b,c] … 再从以 b 为开头的子序列开始遍历 [b], [b,c]
• 根据子序列的长度为标杆，如先遍历出子序列长度为 1 的子序列，在遍历出长度为 2 的 等等
• 以子序列的结束节点为基准，先遍历出以某个节点为结束的所有子序列，因为每个节点都可能会是子序列的结束节点，因此要遍历下整个序列，如: 以 b 为结束点的所有子序列:[a , b], [b] 以 c 为结束点的所有子序列: [a, b, c], [b, c], [ c ]